Diego Alfonso ERBA,
Gustavo NOGUERA, Aldo MANGIATERRA
Adaptado del artículo “Height Reference
for Parcels and Land Objects for the 3D Cadastres Structuring”, publicado y
presentado en el 4th International FIG 3D Cadastre Workshop, 9-11 November
2014 Dubai, United Arab Emirates.
----------------------------------------------------------------------------------------------------------------------
1. INTRODUCCIÓN
El catastro 3D
debe registrar los objetos territoriales con precisión en el espacio y en el
tiempo, identificándolos y ubicándolos geométricamente como volúmenes en un
determinado momento. Un registro 3D permite relacionar objetos territoriales, o
parte de ellos, reposicionarlos retrospectivamente, proyectar modificaciones y
analizar la influencia de nuevos objetos aún antes de que existan a través de
la construcción de escenarios prospectivos.
El catastro 3D,
más allá de las medidas del objeto territorial, debe contar con las tres
coordenadas de un número suficiente de puntos que permitan ubicarlo
espacialmente como bloque en el marco de referencia y a la fecha de medición.
El número de puntos de georreferenciación dependerá de cada caso y será
definido por el profesional de acuerdo a su criterio y experiencia, de manera
que se garanticen los parámetros de precisión establecidos por la norma
catastral.
El
posicionamiento planimétrico de los objetos territoriales no presenta mayor
dificultad una vez que se establece el sistema de referencia geodésico, no
obstante, la definición de la superficie de referencia más adecuada para
determinar las alturas, está aún en discusión.
El presente
trabajo describe distintos sistemas existentes para referenciar las alturas de
parcelas y objetos territoriales, y sus posibles aplicaciones en la
estructuración de catastros 3D. Discute ventajas e inconvenientes en la
utilización de cada uno de ellos para el posicionamiento en el espacio.
A lo largo del
desarrollo se analizan las hipótesis en estudios de caso propios del catastro
3D, sin la pretensión de cubrir la totalidad de los mismos. La teoría
desarrollada es aplicada para posicionar departamentos que forman parte de
edificios de viviendas privadas (parcelas 3D) y elementos de una obra vial
(objetos territoriales 3D), mostrando las correlaciones entre los distintos
sistemas de alturas.
Los
resultados alcanzados en esta investigación permiten afirmar que el
elipsoide de revolución es la superficie más apropiada para referenciar las
alturas de parcelas 3D y de la mayoría de los
objetos territoriales 3D, siendo que para determinados objetos territoriales 3D
puede ser necesario utilizar, además del elipsoide, una superficie
equipotencial para referenciar sus alturas. También permiten
afirmar la posibilidad de construir modelos “locales” de geoide que permitan
convertir diferencias de alturas elipsoidales en diferencias de alturas
geoidales (y viceversa).
Lo aquí
desarrollado cobra mayor importancia a partir de la aplicación del nuevo Código
Civil y Comercial y la consecuente ampliación de derechos reales
2. SISTEMAS DE
ALTURAS PARA CATASTRO 3D
Una superficie de referencia es aquella a
partir de la cual se definen las alturas de puntos en el espacio. Para
establecerla es necesario fijar diferentes parámetros, siendo los planos, los
elipsoides de revolución y las superficies equipotenciales las más comúnmente
usadas.
Un plano horizontal es la superficie de
referencia más simple en términos geométricos y de más fácil comprensión para
los usuarios. Su posición espacial se define como normal a la vertical en un
punto origen y las alturas de los
demás puntos se miden a lo largo de rectas perpendiculares a ese plano. Desde
que, en términos generales, se considera vertical
de un punto a la dirección de la fuerza de gravedad terrestre que pasa por
él, las rectas perpendiculares al plano de referencia que se adopte y las
verticales no necesariamente coinciden. Por otra parte las alturas resultan
válidas sólo para extensiones reducidas puesto que a 1 km de distancia del punto
origen el error altimétrico ya es del orden de los 8 cm debido a la curvatura
terrestre.
Un elipsoide de revolución es una
superficie de referencia de carácter matemático; su centro, orientación,
semieje mayor y aplastamiento son elegidos de tal forma que su aproximación al
geoide sea máxima.
Una superficie equipotencial o superficie
de nivel es siempre perpendicular a la vertical, y dado que la dirección de las
verticales es influenciada por la distribución de masas y por el movimiento
terrestre, esta superficie resulta ser irregular. Se adopta como superficie
equipotencial de referencia al geoide
que es la que mejor se adapta al nivel medio del mar a escala global.
Las distancias
de los puntos en el espacio hasta las superficies de referencia se denominan alturas, aun cuando en el lenguaje
geodésico frecuentemente son denominadas cotas.
Dado que las superficies equipotenciales no son paralelas, el resultado
de una nivelación geométrica dependerá del camino recorrido.
 |
| Figura 1 - Distancia entre superficies equipotenciales |
La Figura
Al variar el itinerario puede variar el resultado. La ambigüedad de las
cotas obtenidas de tal forma conduce a la denominación de alturas brutas.
El concepto de nivel se puede asociar también al concepto de potencial
gravitatorio, puesto que puntos ubicados a mayor altura tienen un potencial
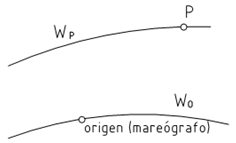
gravitatorio menor. Considerando como superficie equipotencial de referencia al
geoide de potencial W0 (origen del mareógrafo), se define como cota geopotencial del punto P a la
diferencia entre el potencial en W0 y
el potencial de la superficie de nivel que pasa por P (WP).
 |
 |
||
Las cotas geopotenciales determinan rigurosamente la dirección de
escurrimiento del agua entre los puntos y el valor que se obtiene para
cualquier punto es independiente del camino utilizado, razón por la cual en
todos los casos se obtendrá un resultado único. Cabe señalar que las cotas
geopotenciales no representan una longitud sino el trabajo necesario para
trasladar una masa unitaria desde el origen 0 hasta un punto P. Esta última
característica hace que, en la práctica, su utilización no sea conveniente en
levantamientos terrestres.
 |
Para evitar esta limitación, Huerta (2001) nos recuerda la definición de las cotas dinámicas (CD) como el cociente entre la cota geopotencial y un valor de gravedad constante. De esta manera los valores resultantes se expresan como distancias. Normalmente se utiliza el valor de gravedad normal sobre el elipsoide a altitud
Así, las cotas
dinámicas tienen una característica común con las cotas geopotenciales: los
puntos de igual cota pertenecen a la misma superficie equipotencial. Esta
característica hace que, aunque se expresan en unidades de distancia, resulten
insensibles a la convergencia de las superficies de nivel. Para determinar la
cota geopotencial o la dinámica se debe realizar una nivelación geométrica
midiendo a la vez la aceleración de la gravedad (g).
Entendiendo
claramente los conceptos de cotas, pasamos a los conceptos de alturas, las
cuales son utilizadas para el posicionamiento de las parcelas y los objetos 3D.
La
altura ortométrica (H) de un punto ubicado en la superficie
terrestre es la distancia entre él y la superficie equipotencial de referencia
(geoide), medida a lo largo de la dirección de la vertical. Esta altura se obtiene a partir de la cota
geopotencial considerando un valor medio de g, lo que implicaría conocer la
distribución de masas entre el punto en cuestión y su proyección (según la
vertical) sobre el geoide. Esto en rigor resulta imposible, pero se puede
suplir satisfactoriamente por un cálculo utilizando parámetros conocidos.
La altura normal es determinada a partir
de la gravedad normal en vez de un valor medio de g, es decir, surge de un
cálculo que considera un modelo adoptado para el campo gravitatorio terrestre.
La altura normal es un valor que poco difiere de la altura ortométrica (en
general pocos centímetros), y define una nueva superficie de referencia
denominada cuasi-geoide. Se puede afirmar que la separación entre el geoide y el
cuasi-geoide varía (tomando casos extremos) de algunos centímetros a poco más
de un metro. Para la superficie de los océanos el geoide y el cuasi-geoide son
coincidentes

La altura elipsoidal (h) es la distancia entre un punto en el espacio y la superficie del elipsoide, medida
a lo largo de la normal al elipsoide. El Sistema Global de Navegación Satelital
(por su sigla en inglés Global Navigation
Satellite Systems - GNSS) permite conocer esta altura con la precisión que fuere necesaria, inclusive
de hasta pocos mm.
Al vincular h y
H de un mismo punto es posible relacionar el geoide con el elipsoide a través
de la ondulación del geoide (N),
donde: N = h – H. En rigor, aun cuando la vertical
del punto y la normal al elipsoide no son exactamente coincidentes, son tan
próximas que su desvío no influye en el cálculo de N. Navratil & Unger
(2011) afirman que para utilizar nivelación geométrica en la estimación de
diferencias de alturas elipsoidales es necesario conocer el desvío de la
vertical. Esta afirmación es verdadera pero tiene un carácter muy general pues
en la práctica depende de la precisión requerida y de la extensión que se
quiere abarcar.
En
zonas de llanura y en áreas cuyo radio no exceda algunas decenas de kilómetros
es posible obtener modelos locales de geoide que permitan correlacionar las
alturas ortométricas con las alturas elipsóidicas. Esta estrategia puede ser
aplicada tanto en la construcción de un túnel, con posicionamiento satelital
solamente en los extremos y nivelación geométrica en su interior, cuanto en la
construcción de obra vial sobre superficie acuática que imposibilita la
nivelación geométrica (salvo en los extremos). Apelando a una combinación
inteligente de nivelación geométrica, posicionamiento satelital y modelización
geoidal, los resultados pueden ser satisfactorios para el posicionamiento
espacial de esos objetos territoriales.
En
este caso, la expresión a utilizar para calcular desniveles es: (H2-H1)
= (h2-h1) - (N2-N1)
Esa solución fue aplicada durante la construcción de la obra vial que
une las ciudades de Rosario y Victoria, atravesando el delta del río Paraná de 60 km de ancho (Figura 2). Al
comenzar la obra hubo una creciente extraordinaria del río que cubrió de agua
toda el área, lo que hacía casi imposible realizar una nivelación geométrica.
En
ambas cabeceras se midieron las alturas
elipsóidicas y sobre el nivel del mar, y se determinaron los respectivos
valores de N. Se midió también la gravedad en diversos puntos y, apelando a un
modelo de geoide global, se pudo calcular la variación de N a partir del
trazado de un perfil geoidal a lo largo de la traza de la obra. Siguiendo esta
estrategia se pudieron obtener alturas sobre el nivel del mar en cualquier punto de la obra tomando como base el
posicionamiento satelital, satisfaciendo una tolerancia de 10 cm , lo cual se verificó
una vez finalizada la construcción.
Figura 2 – Ubicación del área de estudio,
Rosario, Argentina
Fuente: Google Maps
2.1.
Modelos de
Geoide y Estaciones Permanentes GNSS
Para
relacionar alturas elipsoidales y ortométricas se utilizan modelos de
transformación de alturas denominados modelos de geoide, de los cuales es
posible obtener N para la zona en estudio. Estos modelos pueden obtenerse a
partir de la información de puntos geodésicos con ambas alturas (h y H), que se
encuentran en la zona, generalmente de extensión limitada. Un ejemplo de este
tipo es el Modelo de geoide de la ciudad de Rosario - MGR06 presentado en la Figura 3.
La relación de alturas
elipsoidales y ortométricas puede determinarse también a partir de modelos
globales como el EGM2008 (Earth
Gravitational Model) y EIGEN (European
Improved Gravity model of the Earth by New techniques), los cuales se
construyen generalmente a partir de datos de observaciones de satélites
específicos para este fin, y suelen tener como limitante la definición del
“origen”. Si se cuenta con uno (o varios) puntos con la doble información (h y
H) en la zona, es posible calibrar el modelo global a partir del N de una
estación permanente siendo el resultado útil para una zona amplia en estudio.
Figura 3 - Modelo de geoide de la ciudad de Rosario - MGR06,
Argentina
Fuente: Balbarani et al. (2006)
En la ciudad de
Rosario y zonas aledañas, el EGM2008 fue calibrado con el N de la estación
permanente denominada UNRO, el resultado de este trabajo está representado en la Figura 4.
Figura 4 - EGM2008 calibrado con el N de
estación permanente UNRO
Una estación
permanente consiste en un receptor GNSS rastreando todos los satélites
visibles, en forma continua las 24 hs.,
junto con un sistema de almacenamiento y publicación de los datos (generalmente
a través de Internet, en tiempo real o en forma diferida) de forma que esos
datos estén a disposición de los usuarios.
El conjunto de
las estaciones permanentes conforman una red. En Argentina, la Red Argentina de
Monitoreo Satelital Continuo - RAMSAC está
compuesta por algo más de 70 estaciones y es administrada por el Instituto
Geográfico Nacional - IGN. Para que los datos de las estaciones permanentes
resulten de utilidad a la georreferenciación, las coordenadas geodésicas
(latitud, longitud y altura elipsóidica h) de la estación deben ser conocidas y
publicadas. Si todas las estaciones permanentes contaran con esta información
(h y H) se podría desarrollar de forma bastante simple un modelo geoidal de
alcance regional o bien utilizar el valor de N en la estación para calibrar un
modelo global para la zona de la estación. Contar con la coordenada H en el
mismo punto de la estación sería altamente relevante para el posicionamiento de
objetos territoriales y parcelas 3D.
En
la actualidad muy pocas estaciones cuentan con esa doble altura (h y H) en
América Latina. Se hace una especial recomendación a los Institutos Geográficos
de los países de la región para que traten de determinar y publicar los H de
las estaciones permanentes así como para que obtengan y publiquen g.
3. CASOS DE ESTUDIO
Se presentan a
continuación 2 casos correspondientes a aplicaciones de la teoría desarrollada
los que corresponden a la ciudad de Rosario.
3.1.
Complejo
de edificios “Ciudad Ribera”, Rosario, Argentina
De
acuerdo con la legislación vigente en Argentina, el dominio público en cursos
navegables se extiende hasta la llamada línea
de ribera, la cual corresponde a la que determinan las aguas del río en su
máxima crecida ordinaria. Para la ciudad de Rosario esa cota está oficialmente
establecida en 4.16
metros . Lo singular es que esa altura está referida al
cero del hidrómetro del puerto de Rosario, es decir la superficie de referencia
es estrictamente local.
Figura 5 – Perfil de los alrededores del emplazamiento del
complejo de edificios “Ciudad Ribera”. Localización del límite público-privado y
alturas locales.
La
línea que representa la intersección de la superficie vertical que divide el
dominio privado del público con el terreno puede ser referenciada bajo 3
superficies diferentes, tal como muestra la Tabla 1.
Tabla 1 – Alturas de la línea que
divide el dominio público del privado
Sistema local
|
|
Sistema nacional (altura sobre el nivel del mar)
|
|
Sistema global (altura elipsóidica según modelo de geoide local)
|
Tomando
estas referencias, el terreno natural en los alrededores del Complejo de
edificios “Ciudad Ribera” presenta las alturas local, elipsoidal y ortométrica
descriptas en la Tabla
2.
Tabla 2 – Alturas en el sitio de
emplazamiento de los edificios de “Ciudad Ribera"
Sistema local
|
18,55m
|
Sistema nacional (altura sobre el nivel del mar)
|
22,14m
|
Sistema global (altura elipsóidica según modelo de geoide local)
|
39,10m
|
3.2.
Edificio
“Embarcadero”, Rosario, Argentina
Este
edificio fue sometido al régimen de Propiedad Horizontal (ley nacional No.
13512). El caso fue elegido pues evidencia una situación singular en términos
legales: el subsuelo está destinado a cocheras (dominio privado), pero una
parte de la planta baja, la que no tiene edificación, está sometida a una
servidumbre destinada al uso público, regulado por la Municipalidad de
Rosario.
Como
muestra la Figura
6, el agrimensor estableció un plano local como referencia, atribuyendo 0.00 m de altura en la
planta baja, la cual constituye la referencia de altura para cada parcela
(pública o privada). Aplicando la teoría desarrollada anteriormente, se
determinaron las relaciones entre las alturas local, elipsoidal y ortométrica,
expresadas en la Tabla
3.
La
altura de la base del edificio Embarcadero se obtuvo por nivelación geométrica,
partiendo del punto fijo V1 ubicado a unos 200 metros del mismo. El
V1 corresponde al Relevamiento Costa Norte de Rosario y su altura sobre el
nivel del mar es 23,51 m
(fuente: Catastro de la
Municipalidad de Rosario). La altura elipsóidica se obtuvo
utilizando el valor de N = 16,96
m proporcionado por el modelo geoidal de Rosario MGR06.
Tabla 3 – Relación entre las
alturas alrededor del edificio “Embarcadero”
Sistema local
|
|
Sistema nacional (altura sobre el nivel del mar)
|
|
Sistema global (altura elipsóidica según modelo de geoide local)
|
Figura 6 – Corte longitudinal del edificio Embarcadero y alturas locales de
los objetos
4. CONCLUSIONES Y RECOMENDACIONES
El catastro 3D
es un registro que contiene la posición espacial de los objetos territoriales y
parcelas en el espacio, definida con precisión adecuada y en un momento
determinado (el de la medición). El principal problema de un catastro 3D es la
definición de las alturas de las parcelas y los objetos puesto que la cultura
de catastros 2D ya ha desarrollado diferentes métodos para posicionamiento de
las proyecciones de las parcelas.
Un plano sería
eficiente como superficie de referencia vertical para estructurar un catastro
3D de áreas cuyas extensiones no superen 1 km , pero esta superficie no es global y tiene
aplicaciones limitadas, no se podría usar con eficiencia en la mayoría de las
jurisdicciones latinoamericanas.
La altura
elipsoidal es más apropiada para la mayoría de los casos puesto que no presenta
ambigüedades y puede obtenerse con precisión adecuada al catastro en un momento
determinado. Los movimientos tectónicos no constituyen un problema puesto que,
como sus efectos son conocidos a partir de las mediciones, es perfectamente posible
correlacionar las coordenadas de un mismo objeto en el espacio en dos épocas
distintas. En otras palabras, las coordenadas elipsoidales brindan información
más confiable que el más robusto de los mojones que materializan límites.
Definitivamente
la altura elipsoidal es la que resuelve la necesidad esencial de registrar
Parcelas 3D, pero no es suficiente para atender otras necesidades. En los casos
en que sea menester conocer el desplazamiento de las aguas debe utilizarse,
junto a la elipsóidica, la altura ortométrica para posicionar los objetos
territoriales.
Se puede
concluir que no es posible fijar una única precisión para las referencias de
alturas, sino que ésta varía con el carácter mismo de los objetos catastrales.
Además vale una aclaración: este trabajo se refiere solamente a las tolerancias
en el posicionamiento espacial, considerado al objeto catastral como un bloque,
excluyendo del análisis las precisiones requeridas en las medidas internas del
objeto territorial.
Cada
repartición a cargo del catastro 3D deberá estipular, en el ámbito de su
jurisdicción, cuales son las tolerancias que se deben respetar. Consideramos
que para inmuebles urbanos la tolerancia espacial para la georreferenciación
puede estar en el orden de los 10
cm . Una tolerancia similar correspondería para los
conductos subterráneos de servicios públicos, por ejemplo los cloacales, las
redes de gas o energía eléctrica, siempre en el ámbito urbano. Para propiedades
rurales la precisión dependerá de la zona en cuestión.
5. REFERENCIAS BIBLIOGRÁFICAS
Balbarani, Sebastián; Banchio, Ulises & Piancatelli,
Federico (2006). Modelo geoidal para la ciudad de Rosario. Universidad
Nacional de Rosario, trabajo final de la carrera de Agrimensura,
Rosario, Argentina
Huerta, Eduardo (2001). Sistemas de alturas. In: Georreferenciación. Revista TEMAS DE
GEOCIENCIA Nº7. Editorial de la Universidad Nacional de Rosario, Rosario,
Argentina.
Navratil, Gerhard & Unger, Eva-Maria (2011). Height Systems for 3D Cadastres. In: 2nd International Workshop on 3D Cadastres, Delft ,
the Netherlands
Huerta, E.; Mangiaterra, A. & Noguera, G.
(2005). GPS Posicionamiento Satelital.
Editorial de la
Universidad Nacional de Rosario, Rosario, Argentina.
Leick, Alfred (2004). GPS Satellite Surveying. Ed. John Wiley and Songs, New Jersey ,
USA
Mônico, João Francisco
Galera (2008). Posicionamento pelo GNSS,
Descrição, fundamentos e aplicações. Editora UNESP, São Paulo, Brasil.
Nikolaos K. Pavlis, Simon
A. Holmes, Steve C. Kenyon, John K. Factor. The development and
evaluation of the Earth Gravitational Model 2008 (EGM2008). Journal of Geophysical Research:
Solid Earth (1978-2012) Volume 117, Issue B4, April 2012
Facultad de Ciencias Astronómicas y Geofísicas,
Departamento de Astrometría. Informe
Técnico para Usuarios de tdaGEOBA. Universidad Nacional de La Plata. Disponible
en: http://geoweb.fcaglp.unlp.edu.ar/static/tdaGEOBA.pdf
AGRADECIMIENTOS
A los colegas y amigos por
sus contribuciones: Pascual
Calvo, Director de Catastro y Raúl Álvarez, Presidente Servicio
Público de la Vivienda
y el Hábitat, ambos de la
Municipalidad de Rosario, Argentina, y Eduardo Huerta, ex profesor de la Universidad Nacional
de Rosario.
SOBRE
LOS AUTORES
Diego
A. Erba
Land
Surveyor Engineering from Universidad Nacional de Rosario, Argentina. Doctor in Surveying Sciences from Universidad Nacional
de Catamarca, Argentina Cape Verde ,
and for the Ministry of Housing and Urban Development of Ecuador
Gustavo Noguera
Agrimensor
egresado de la
Universidad Nacional de Rosario, Argentina.
Profesor
titular de cátedras de Topografía y Posicionamiento Satelital en la carrera de
Agrimensura de la
UNR. Actualmente director e investigador del Grupo de
Geodesia Satelital de Rosario.
Aldo O. Mangiaterra
Agrimensor e Ingeniero
Geógrafo de la
Universidad Nacional de Rosario, Argentina. Ex profesor
titular en la misma Universidad. Fue director del Grupo de Geodesia Satelital
de Rosario. Se desempeñó en diversos ámbitos profesionales en la actividad
privada. Actualmente es investigador externo del Grupo de Geodesia Satelital de
Rosario.






No hay comentarios:
Publicar un comentario
Introducir comentario